This is a new version of an old article about lenses and prisms in Swift. This one contains many updates and more precisely reflects how I actually use these things in my work. This is also based on a talk I gave at iOSDevUK 2017 and Mobilization Conference 2017. I’m keeping the old article in draft as reference.
In date Sep 8 2018 I modified the article further, by including Affine in the discussion, again to reflect my current work better.
The concept of functional lens has become pretty popular in functional programming circles, and there are already good contributions for applying lenses to other, traditionally imperative/OO contexts, like Javascript. Brandon Williams has done an excellent job in introducing lenses to the Swift community, and in showing practical examples when working with something like UIView, a radically OOP construct that an iOS developer has to work with on a daily basis.
I’d like to offer a more in depth view on why lenses can be useful in Swift, and also talk about a related concept called Prism: it’s likely that everyone that’s interested in lenses has heard about prisms but it seems like, while the basic intuition behind a lens can be grasped, the one behind a prism is kind of obscure. But before that, it might be important to discover again the concept of Lens: I’d like to do that because, by reading the comments for this video, I understand that there’s some confusion, mixed with the usual hostility towards functional programming concepts by some OOP people (luckily, a minority) who consider functional programming pointlessly complex: it’s really the opposite, that is, it’s simple but initially hard to grasp. And simple vs. complex is not the same thing as easy vs. hard.
So, let’s start from the beginning and talk about lenses, but in a more pragmatic way, that is, let’s consider some practical problems and see if a traditional, idiomatic (and imperative) Swift approach can be enough or not. Most of the code from this post is available in a Swift Playground, and I strongly recommend to follow the Playground while reading the post, even if I’m still going to recall most of the code here.
Functional Getters and Setters
If you google “functional lens” you’re probably going to end up with a definition like “functional getter and setter”: in this context the word “functional” really means “immutable”. There are many advantages in using immutable data models - I’m not going into it for this article - but modifying immutable models (i.e. generating new models with something changed) can be a chore, because the whole model must be reconstructed by taking the previous values where they didn’t change, and setting the new values where they did. But Swift offers particular kinds of types, called “value types”, that have value semantics, which basically means that they have no identity and only represent a “value”, i.e., some kind of “information” that is implicitly immutable: a piece of information cannot change, but new information can be created, rendering the previous obsolete.
For example, a Int is a value type: if I have a 2, and I’m adding 1, I’m not mutating the 2... I’m creating a new instance called 3. If it seems obvious it’s because it is obvious for a type like Int, but in Swift we can also define complex types that have the exact same behavior.
Swift struct and enum are value types: if I give you an instance of a struct, it’s like I’m giving you a copy of my instance, which is not going to be mutated in any way, no matter what you do with your copy. This has many advantages and allows to safely reason about code. An interesting consequence is that one can safely define structs with var properties, because if I set a new value for a property of a struct, what Swift really does under the hood is generating a whole new reference to that instance, such that others referring to it won’t see any change.
For this reason, if I define in my code a struct that have memberwise initializers - that is, they can be constructed with any possible value for the properties - I usually set all the properties as var. There are cases where you still want the let: maybe the struct cannot be constructed with any value for the properties (thus, some mutations wouldn’t make sense), or maybe you really need a class for a model. Anyway, in this article’s code all the model structs will have var properties.
For all these reasons I don’t think that just the definition “functional getters and setters” is going to be useful for lenses and prisms, especially in languages that offer flexible value types like Swift. What makes these ideas interesting is their composability, that allows for building powerful abstractions, as we’ll see.
A matter of relationship
Lenses and prisms (and programming with optics in general) allow us to establish relationships between data structures. In particular, a lens is called like that because it allows to focus on a specific part of a data structure, and consequently to act on that part, like retrieving it, or modifying it causing a modification of the whole data structure. A prism is a similar concept, but it works for sum types, that in Swift are represented via enum. Types like class and struct, that have properties (even a simple tuple), are called product types and are manipulated by lenses; while sum or coproduct types are types like enum, that have cases, and are manipulated by prisms.
Let’s see it graphically:
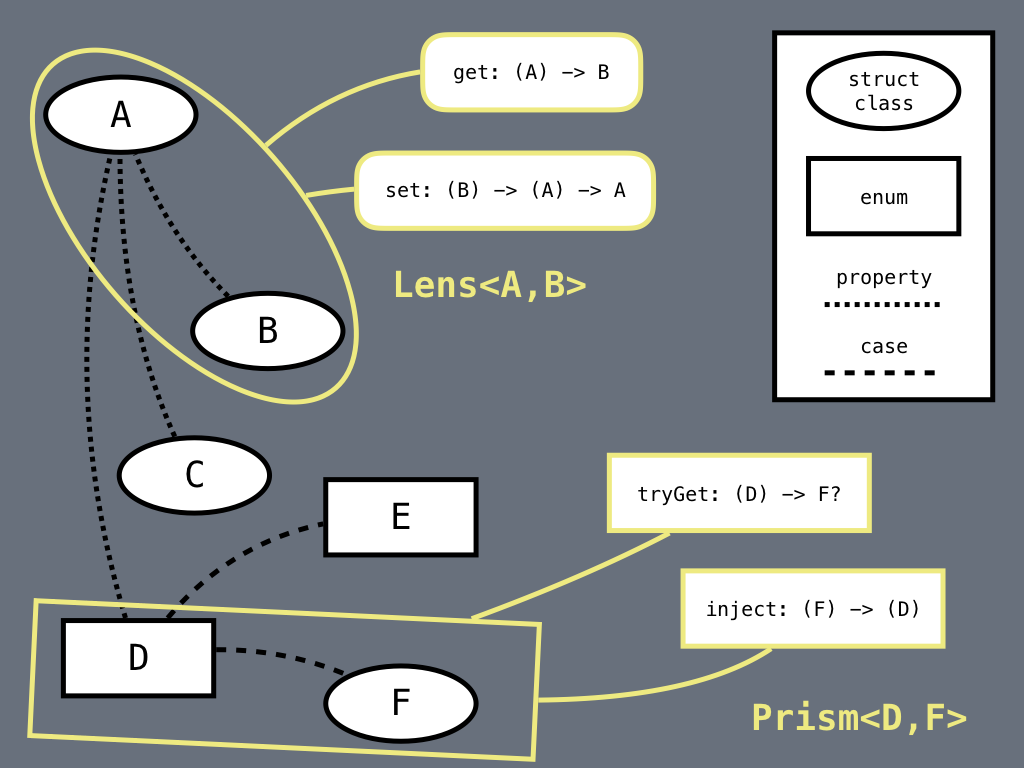
In the image we can see a schematic representation of a generic data structure: ovals are struct or class types, thus, types with properties; rectangles are enum types; dotted lines are properties; dashed lines are cases for enums.
To define a Lens from the type A, that contains instances of the types B, C and D, to one of the contained types, for example B, I need two functions:
- a function called
get that, given an A, will return a B;
- a function called
set that, given a B, will return a transforming function for A, i.e., a function of type (A) -> A.
This implies that Lens is parametrized by two types, the type on which I’m applying the lens, usually referred as Whole, and the type onto which the lens is focusing, called Part. Thus, a full generic representation of a lens can be given like the following:
struct Lens<Whole,Part> {
let get: (Whole) -> Part
let set: (Part) -> (Whole) -> Whole
}
A Prism is the same for coproducts. We can define a prism from D (an enum) to F (the associated type to one of its cases). What’s a get in this case? It’s a function that takes a D and tries to yield a F: I said “tries” because a F can only be retrieved if the D instance is in the right case, otherwise we can simply return nil. That’s why the get for prisms is a tryGet, that returns a Part?. About the set, given a F we can completely reconstruct a D via the case function, so its more like an inject, in which we produce a new D without any knowledge of the previous one. That being said, a nice representation of Prism is the following:
struct Prism<Whole,Part> {
let tryGet: (Whole) -> Part?
let inject: (Part) -> Whole
}
There are actually many ways to define lenses and prisms, and the code I showed defines a very simple representation that I find most useful in my Swift code. Maybe in future articles I’ll explore different representations, but my intention is to give a pragmatic approach, based on what seems useful in day-to-day Swift code, and what I actually use in my own code.
I’ll spend a few more words on Prism<Whole,Part>, with a practical example. Suppose I have the following data structure:
enum ViewState<T> {
case empty
case processing(String)
case failed(Error)
case completed(T)
}
ViewState<T> represents the model for a view that can be in many states, depending on the progress of a particular process: for example, the process could fail, yielding an Error, or could complete successfully, with some generic T value. Let’s define a Prism on ViewState<T>: because it has 4 cases, we can define 4 prisms. For example, for the processing case we can define a prism where the Whole is ViewState<T> (as for any prism defined on this data structure) and the part is String, i.e., the associated type to the processing case. The final type of this prism will then be Prism<ViewState<T>,String>. Notice that a prism defined on the empty case would be of type Prism<ViewState<T>,()>, because () (or Void in Swift) is the implicit associated type of that case.
From View to Model
As many have probably noticed, the perfect use case for lenses and prisms is when we need to act on a tree-like data structure, where many parent-child relationships are established: for each parent-child pair we can define a lens or a prism, depending on the type of the parent (product or coproduct). As iOS developers (or mobile developers in general) we deal with one of these structures on a daily basis, and it’s the view hierarchy. While we could define lenses directly on UIView and on its subclasses, I find it preferable to work with view models, that is, objects that represent views but are not view themselves. I’m not strictly talking about the Model-View-ViewModel architectural pattern, in which the ViewModel could be a mutable class with identity and logic: I’m simply referring to using structs and enums to mediate the content of views, something I could refer to as functional ViewModel. A ViewModel like this is dumb, has no logic, only data, and is acted upon from the outside with functions, functions like the ones defined in lenses and prisms.
Let’s see an example:
struct LoginPage {
var title: String
var credendials: CredentialBox
var buttonState: ViewState<Button>
}
struct CredentialBox {
var usernameField: TextField
var passwordField: TextField
}
struct TextField {
var text: String
var placeholder: String?
var secureText: Bool
}
struct Button {
var title: String
var enabled: Bool
}
LoginPage is a model for a login page (which is probably going to be a UIViewController in a iOS app), with all its parts: it includes a title that’s simply a String, a CredentialBox struct represented by two TextField that are themselves structs, and a buttonState that’s represented by a ViewState<Button> where Button is another struct. Everything here is var because any of these models can be constructed with any value, and any property can change in any way at any time. But, because we’re dealing with value types, mutating this LoginPage actually means creating a new reference, and that’s only going to be possible if we assign an instance of LoginPage to a variable, annotated with var.
Adding lenses to these structs is simple, and there are many ways to do that. One possible way is to extend each type with a nested type called lens that’s going to act as namespace, and then defining all the lenses as static properties of this lens, like in the following example:
extension CredentialBox {
enum lens {
static let usernameField = Lens<CredentialBox,TextField>.init(
get: { $0.usernameField },
set: { part in
{ whole in
var m = whole
m.usernameField = part
return m
}
})
}
}
As you can see, CredentialBox.lens.usernameField is a lens from CredentialBox to TextField, and because it’s a static property, only an instance of this lens is going to be alive in the entire lifecycle of the application: it’s simply something always available, that can be referred when needed.
The implementation is trivial, there’s really only one sane way to write this: the get function simply gets the value from the usernameField property, while the set grabs a var reference to the whole that’s passed in, mutates it and then returns it: we can do this because usernameField is defined as var in CredentialBox. Notice that the set function is a higher-order function, because it takes a value and returns a new function: we generally want this kind of thing for the set part of a lens, so that we can prepare a function that will transform the Whole with a new Part.
The story is similar for Prism. For example, we might want to the define the Prism for the processing case in ViewState<T>:
extension ViewState {
enum prism {
static var processing: Prism<ViewState,String> {
return Prism<ViewState,String>.init(
tryGet: {
guard case .processing(let message) = $0 else {
return nil
}
return message
},
inject: { .processing($0) })
}
}
}
Unfortunately, with this strategy, we cannot assign the Prism to a stored static property (because ViewState is a generic type): not a big deal, we’ll use a computed property (still static). Again, the implementation is trivial, there’s only one sane way to write this.
Let’s do this
Suppose we want to modify a current instance of LoginPage. A new set of values is represented by the following tuple:
let initialState = (
title: "Welcome back!",
username: savedUsername,
buttonState: ViewState<Button>.completed(Button.init(
title: "Login",
enabled: false)))
initialState contains a bunch of initial settings for the LoginPage: savedUsername might be the username string stored in the UserDefaults.
Because our LoginPage is mutable - in the sense we discussed earlier for value types, that is, not really mutable but it can be manipulated like it was - we can simply do this:
var m_newModel = oldModel
m_newModel.title = initialState.title
m_newModel.credendials.usernameField.text = initialState.username
m_newModel.buttonState = initialState.buttonState
The problem with this approach, which is of course the most basic one for var instances, is that we’re not clearly representing the relationship between the LoginPage and its parts: we’re directly accessing the properties of the model, and in the case of the username text we need to call 3-levels deep of properties (that is, .credendials.usernameField.text). It would be really useful if we had objects that encapsulate the access to properties at any level, for example if we were able to encapsulate the access to the username field text, that is, the relationship with the LoginPage, such that if something changes in the future for this chain of relationships, nothing is going to break in the place where we use the object to manipulate the property itself.
A Lens does exactly this: encapsulates the relationship between a data structure and one of its parts. But for now we only defined lenses from a type to its direct properties. To represent with a lens something like .credendials.usernameField.text we need to compose lenses with matching Part/Whole parameters. What I mean is something like this:
Lens<A,B> + Lens<B,C> = Lens<A,C>
If a lens’ Part is the same as another lens’ Whole we can chain them together, generating a single lens that goes one level deeper in the data structure represented by the first lens’ Whole. It turns out that we can always do this in a completely generic way, we only need the types to match correctly. In fact, we can extend both Lens and Prism with a then function that will take another lens/prism for which the Whole is the same as the first lens/prism Part, and return a new lens/prism that will cover the extended range of types:
extension Lens {
func then<Subpart>(_ other: Lens<Part,Subpart>) -> Lens<Whole,Subpart> {
return Lens<Whole,Subpart>(
get: { other.get(self.get($0)) },
set: { (subpart: Subpart) in
{ (whole: Whole) -> Whole in
self.set(other.set(subpart)(self.get(whole)))(whole)
}
})
}
}
The implementation seems complex, in particular the line self.set(other.set(subpart)(self.get(whole)))(whole), but actually there’s really only one sane way to write this: the types really guide the implementation here, and if it compiles it’s almost certainly going to work. Actually, the only other option for implementing the set function so that Swift compiles is by naively returning the whole input unchanged, which is of course wrong.
We can do the same for Prism:
Prism<A,B> + Prism<B,C> = Prism<A,C>
extension Prism {
func then<Subpart>(_ other: Prism<Part,Subpart>) -> Prism<Whole,Subpart> {
return Prism<Whole,Subpart>(
tryGet: { self.tryGet($0).flatMap(other.tryGet) },
inject: { self.inject(other.inject($0)) })
}
}
I actually prefer to use an operator for composing lenses and prisms this way, the .. operator, which can be read as and then: A..B would be read as A, and then, B.
precedencegroup LeftCompositionPrecedence {
associativity: left
}
infix operator .. : LeftCompositionPrecedence
extension Lens {
static func .. <Subpart> (lhs: Lens<Whole,Part>, rhs: Lens<Part,Subpart>) -> Lens<Whole,Subpart> {
return lhs.then(rhs)
}
}
extension Prism {
static func .. <Subpart> (lhs: Prism<Whole,Part>, rhs: Prism<Part,Subpart>) -> Prism<Whole,Subpart> {
return lhs.then(rhs)
}
}
Now we can simply grab some lenses:
let titleLens = LoginPage.lens.title
let usernameTextLens = LoginPage.lens.credentials..CredentialBox.lens.usernameField..TextField.lens.text
let buttonStateLens = LoginPage.lens.buttonState
A very ugly way to use these lenses to modify our original model would be to apply their set function over and over again on oldModel: because set, applied to a Part, returns a function that transforms the Whole, we can generate these (Whole) -> Whole functions and apply them one after the other to the oldModel. The resulting code is nothing to be proud of:
let newModel = titleLens.set(initialState.title)(usernameTextLens.set(initialState.username)(buttonStateLens.set(initialState.buttonState)(oldModel)))
It would useful if we were able to combine again these lenses, but in a different way: these lenses all share the same Whole, but focus on different Parts. The composition we need is something like this:
Lens<A,B1> + Lens<A,B2> = Lens<A,(B1,B2)>
Prism<A,B1> + Prism<A,B2> = Prism<A,Either<B1,B2>>
The resulting lens will focus on both B1 and B2, while the resulting prism will focus on either B1 or B2; to represent this exclusive or relationship for Prism I used a very simple Either enum:
enum Either<A,B> {
case left(A)
case right(B)
}
Can we combine lenses and prims generically in this way? Of course we can. I like to call this function zip for both Lens and Prism:
extension Lens {
static func zip<Part1,Part2>(
_ a: Lens<Whole,Part1>,
_ b: Lens<Whole,Part2>)
-> Lens<Whole,(Part1,Part2)>
where Part == (Part1,Part2)
{
return Lens<Whole,(Part1,Part2)>(
get: { (a.get($0),b.get($0)) },
set: { parts in { whole in b.set(parts.1)(a.set(parts.0)(whole)) } })
}
static func zip<A,B,C>(_ a: Lens<Whole,A>, _ b: Lens<Whole,B>, _ c: Lens<Whole,C>) -> Lens<Whole,(A,B,C)> where Part == (A,B,C) {
return Lens<Whole,(A,B,C)>(
get: { (a.get($0),b.get($0),c.get($0)) },
set: { parts in { whole in c.set(parts.2)(b.set(parts.1)(a.set(parts.0)(whole))) } })
}
}
extension Prism {
static func zip<Part1,Part2>(
_ a: Prism<Whole,Part1>,
_ b: Prism<Whole,Part2>)
-> Prism<Whole,Either<Part1,Part2>>
where Part == Either<Part1,Part2>
{
return Prism<Whole,Either<Part1,Part2>>(
tryGet: { a.tryGet($0).map(Either.left) ?? b.tryGet($0).map(Either.right) },
inject: { part in
switch part {
case .left(let value):
return a.inject(value)
case .right(let value):
return b.inject(value)
}
})
}
}
I also gave a definition for zip and 3 lenses (of course it can be done for any number of lenses), because this is the one we’re going to use in our example. We can finally define our initialStateLens:
let initialStateLens = Lens.zip(
titleLens,
usernameTextLens,
buttonStateLens)
let newModel = initialStateLens.set(initialState)(oldModel)
initialStateLens encapsulates the entirety of the relationships between data types that we need to apply to the oldModel to get the new one.
What about prisms? Prisms are for enums, so in our example we’re probably going to need them when working with the button state. Suppose for example that we’re in the processing state, so we’re currently showing a message to the user (like “Please wait”). We’d like to modify the LoginPage by setting a new message as time passes, considering the logic expressed by the following function:
func advanceProcessingMessage(_ previous: String) -> String {
switch previous {
case "":
return "Please wait"
case "Please wait":
return "Almost there"
case "Almost there":
return "ALMOST THERE"
default:
return previous + "!"
}
}
This is just a pure function, expressing a simple, isolated piece of logic. But this is not a pure set: it actually depends on the previous value. Both lens’ set and prism’s inject don’t give access to the previous value, but only allow to modify a data structure with a brand new value. We need some kind of modify function (sometimes called over) that instead of taking a new Part to yield a transformation of the Whole, takes a transformation of the Part, i.e., a function of type (Part) -> Part. Can we write this modify function in a completely generic way? Yep:
extension Lens {
func modify(_ transform: @escaping (Part) -> Part) -> (Whole) -> Whole {
return { whole in self.set(transform(self.get(whole)))(whole) }
}
}
extension Prism {
func tryModify(_ transform: @escaping (Part) -> Part) -> (Whole) -> Whole {
return { whole in self.tryGet(whole).map { self.inject(transform($0)) } ?? whole }
}
}
Notice that, for Prism is tryModify: this is because it will only modify an instance of an enum if it’s in the right case; if it’s not, the resulting (Whole) -> Whole function will be an identity, i.e., a function that does nothing on the input, and simply returns it.
Now, we have a lens from LoginPage to ViewState<Button>, and a prism from ViewState<Button> to String: can we compose them? Because composition has been the main point here from the very start of the article: combining small, simple things to form more complex but more useful things. Unfortunately there’s really no easy way to combine a lens and a prism, at least considering the representation we gave for them. Luckily, we really don’t care, because under the hood we’re simply dealing with pure functions, that compose if the types they act upon compose. By composing functions I mean something like this:
(A -> B) + (B -> C) = (A -> C)
This kind of composition can always be done, no matter what A, B and C are, and will always produce something meaningful if the functions involved are pure, which means that they have no side-effects, and that for the same input they’ll always return the same output. A classic way of composing functions is by using a dot operator •, defined like the following:
infix operator •
func • <A,B,C> (
_ left: @escaping (B) -> C,
_ right: @escaping (A) -> B)
-> (A) -> C
{
return { left(right($0)) }
}
The operator will simply apply both functions to a certain argument, one after the other. Now that we have a way to easily compose functions, we can generate a function that will modify the entire login page by applying a modification of the message for the processing state:
let buttonStateLens = LoginPage.lens.buttonState
let processingPrism = ViewState<Button>.prism.processing
let onProcessing = buttonStateLens.modify • processingPrism.tryModify
From a completely generic standpoint, we’re obtaining the onProcessing function with a composition like the following:
(B -> B) -> (A -> A) • (C -> C) -> (B -> B) = (C -> C) -> (A -> A)
Or, by using the actual types:
(ViewState<Button> -> ViewState<Button>) -> (LoginPage -> LoginPage) • (String -> String) -> (ViewState<Button> -> ViewState<Button>) = (String -> String) -> (LoginPage -> LoginPage)
Thus, the result is a function of type (String -> String) -> (LoginPage -> LoginPage), that is, a higher-order function that takes a function that modifies a String (our processing message) and returns a function that modifies the entire LoginPage: in a way, this function takes a transformation of a small subpart of the data structure, and lifts it into a transformation of the whole structure.
Finally, we can apply our onProcessing function like the following:
let newModel = onProcessing(advanceProcessingMessage)(oldModel)
It’s all nice and well, but...
Up to this point we’ve been working mostly with types: words like lens, prism, zip, tryModify et cetera, are really just conventions for expressing what is really expressed by the types involved, in particular by the types of the functions that we composed and applied to our data structures. Types here are the only interface that we used to combine together the various pieces, and if types don’t change, nothing should break. Unfortunately, types might be not enough.
If I give you a lens, what I’m really giving you is functions based on a pair of types, a Whole and a Part: but just the interface doesn’t make sure that the lens is going to work as intended (for example, that it’s actually going to modify the data structure as we’d expect). How can we be sure that a lens or a prism behave properly? The answer is LAWS.
As programmers we don’t frequently talk about what laws or axioms our code is supposed to respect. But we really should. In fact, a discussion about laws is always needed when we’re building a large system from small pieces, because we need to trust the pieces: we wouldn’t be able to reason about code at all if we weren’t able to assert some properties on our pieces. And actually, when we write tests we’re really asserting that certain invariants are going to hold: for example, that a function called with a specific input will always return a specific output. But the problem with tests is that, usually, the underlying axioms that we’re asserting are implicit in the tests, meaning that we’re not really defining them. A nasty consequence of this is that we could end up writing tests that are ineffective (because we’re not really testing against all the laws) or redundant (because a certain law is already made sure by another test). Let’s define this axioms explicitly for lenses and prisms.
For a very well-behaved Lens we need to prove 3 laws:
getSet: if I get a B from a data structure A, and then I set it back, A is not going to change;setGet: if I set a B into a data structure A and then I get it back, the retrieved B must be equal to the initial one;setSet: set is idempotent, meaning that if I set a B into an A multiple times, it’s going to be exactly as if I set it just once.
A well-behaved Prism has similar laws, that basically state that a full instance of the Whole is completely defined by each and everyone of its Parts:
tryGetInject: if I’m able to tryGet a B from an A, injecting it back yields exactly the same A;injectTryGet: if I construct an A by injecting a B, I must be able to tryGet exactly the same B.
Once we have these laws defined, we can test lenses and prisms by asserting that the laws hold for any possible Whole and Part. I like to implement these kind of assertions as functions that return true or false, defined in a Law namespace, like the following:
struct LensLaw {
static func setGet<Whole, Part>(
_ lens: Lens<Whole,Part>,
_ whole: Whole,
_ part: Part)
-> Bool where Part: Equatable
{
return lens.get(lens.set(part)(whole)) == part
}
}
This LensLaw.setGet function takes a Lens<Whole,Part> as argument, together with a Whole and a Part, and returns a Bool simply by equating the retrieved part to the initial part (in fact, Part must be Equatable for the law to be asserted). Calling this function with a certain Whole and Part will only prove that the lens behaves for those specific instances. What we want to do instead is to call this function with many random instances of Whole and Part, and then check if the function always returns true. This procedure is usually called property-based testing, and can be performed with libraries like SwiftCheck.
For example, using SwiftCheck we could write a test case like the following:
func testLensBehaves() {
let lens = Whole.lens.someProperty
property("Whole.lens.someProperty respects the setGet law") <- forAll { (whole: Whole, part: Part) in
LensLaw.setGet(lens,whole,part)
}
}
SwiftCheck is going to call the closure passed to forAll many times, with many different random values of whole and part (the types must conform to certain protocols, please refer to SwiftCheck documentation for the details), and the test will pass only if the closure returns true at each call.
As always, boilerplate
Many of you might have noticed that the code for implementing lenses and prisms for our types is basically boilerplate: it has always the same structure, with only the names of properties and types changing. This has two implications:
- we don’t really need to test the code for trivial lenses and prisms, that is, lenses and prisms that are defined for properties and cases;
- we can automatically generate code with tools like Sourcery.
For lenses in particular, starting from Swift 4, we don’t even need code generation thanks to the new KeyPath type. From a WritableKeyPath<Root,Value> we can always generate a Lens<Root,Value> with code like the following:
extension WritableKeyPath {
var lens: Lens<Root,Value> {
return Lens<Root,Value>.init(
get: { whole in whole[keyPath: self] },
set: { part in
{ whole in
var m = whole
m[keyPath: self] = part
return m
}
})
}
}
let passwordLens = (\LoginPage.credentials.passwordField.text).lens
Unfortunately, this is not going to work if the Value property onto which the lens is focusing is let, thus immutable - we won’t get a WritableKeyPath for it - and also KeyPath is not available for enums, so code generation is still our friend here.
For example, the following template will generate the lenses for all the properties of structs, equipped with a memberwise initializer, annotated with the comment //sourcery: lens (please refer to Sourcery documentation for more info):
{% for type in types.structs|annotated:"lens" %}
extension {{ type.name }} {
enum lens {
{% for variable in type.variables|!static|!computed %}
static let {{ variable.name }} = Lens<{{ type.name }}, {{ variable.typeName }}>(
get: { $0.{{ variable.name }} },
set: { part in
{ whole in
{{ type.name }}.init({% for argument in type.variables|!static|!computed %}{{ argument.name }}: {% if variable.name == argument.name %}part{% else %}whole.{{ argument.name }}{% endif %}{% if not forloop.last %}, {% endif %}{% endfor %})
}
}
){% endfor %}
}
}
{% endfor %}
A slightly different template is going to be needed if the type is generic (because we won’t be able to add static stored properties to it), but that’s the general strategy.
Tests are still going to be important, though, when we need to prove that functions like then and zip work as intended. Also, in some cases we really want to write some lenses and prisms manually, and consequently we’re really interested in testing them. For example we can define prepared lenses for particular data structures, like a Dictionary. I frequently use the following Lens, that focuses on a particular key of a dictionary:
extension Dictionary {
static func lens(at key: Key) -> Lens<Dictionary,Value?> {
return Lens<Dictionary,Value?>(
get: { $0[key] },
set: { part in
{ whole in
var m_dict = whole
m_dict[key] = part
return m_dict
}
})
}
}
This seems perfectly fine, but I want to be able to test this, and laws are the answer.
Notice that the returned lens here is of type Lens<Dictionary,Value?>: the Part is Optional and this is going to give us trouble in composition. What I mean is, we were able to generically compose lenses like this:
Lens<A,B> + Lens<B,C> = Lens<A,C>
But here, we could deal with something like this:
Lens<A,B?> + Lens<B,C> = ?
B? and B are not the same, so the regular composition doesn’t work. A Lens is simply not enough for this, we cannot make a lens failable while keeping it a proper lens that follows the laws. But it turns out that there’s another optic that works exactly like a failable lens, and it’s called Affine:
struct Affine<Whole,Part> {
let tryGet: (Whole) -> Part?
let trySet: (Part) -> (Whole) -> Whole?
}
An Affine<Whole,Part> looks exactly like the mix of a lens and prism, for it has tryGet, like a prism, while the set is actually a trySet that tries to set a value, but can fail, and that’s reflected but the returned type, that is, Whole?.
As an example, we can define an Affine on the element at a certain index in an array:
extension Array {
static func affine(at index: Int) -> Affine<Array,Element> {
return Affine<Array,Element>.init(
tryGet: { array in
guard array.indices.contains(index) else { return nil }
return array[index]
},
trySet: { element in
{ array in
guard array.indices.contains(index) else { return nil }
var m = array
_ = m.remove(at: index)
m.insert(element, at: index)
return m
}
})
}
}
Affines compose like lenses and prisms, with the then method:
extension Affine {
func then <Subpart> (_ other: Affine<Part,Subpart>) -> Affine<Whole,Subpart> {
return Affine<Whole,Subpart>.init(
tryGet: { s in self.tryGet(s).flatMap(other.tryGet) },
trySet: { bp in
{ s in
self.tryGet(s)
.flatMap { a in other.trySet(bp)(a) }
.flatMap { b in self.trySet(b)(s) }
}
})
}
}
Affine must follow laws very similar to those of Lens, that is, trySetTryGet, tryGetTrySet and trySetTrySet. Interestingly, we can turn any lens or prism into an affine:
extension Lens {
func toAffine() -> Affine<Whole,Part> {
return Affine<Whole,Part>.init(
tryGet: self.get,
trySet: self.set)
}
}
extension Prism {
func toAffine() -> Affine<Whole,Part> {
return Affine<Whole,Part>.init(
tryGet: self.tryGet,
trySet: { part in self.tryModify { _ in part } })
}
}
Now we can solve the problem related to composing Lens<A,B?> with Lens<B,C>. We’ll leverage a very specific prism, that is, the prism on an Optional<Wrapped>:
extension Optional {
static var prism: Prism<Optional,Wrapped> {
return Prism<Optional,Wrapped>.init(
tryGet: { $0 },
inject: Optional.some)
}
}
Now we simply need a little algebra:
/// we cannot do this
Lens<A,B?> + Lens<B,C> = ?
/// but we can stick a prism in the middle
Lens<A,B?> + Prism<B?,B> + Lens<B,C>
/// we then turn everything into an affine
Affine<A,B?> + Affine<B?,B> + Affine<B,C>
/// finally, we compose the affines
Affine<A,B?> + Affine<B?,B> + Affine<B,C>
--> Affine<A,B> + Affine<B,C>
--> Affine<A,C>
/// the final result goes from A to C, with no optionals
Affine<A,C>
Notice that, because we can always turn a lens or a prism into an affine, it means that we can compose lenses with affines and prisms with affines, which means that, finally, the affine is the result of the composition between a lens and prism, which is maybe the big piece that was still missing:
Lens<A,B> + Prism<B,C> = Affine<A,C>
Prism<A,B> + Lens<B,C> = Affine<A,C>
Affine solves our nullability problem by employing a special focusing strategy: it either focuses on something or on nothing, and this idea is encoded in its very semantics. Notice that, once you’re in Affine, you simply can’t get out, because everything will be considered nullable from that on, and there’s no alternative in terms of optics: a weak link makes for a weak chain. To avoid using Affine we need to avoid Optional altogether, but usually Optional is exactly what we want, because it better expresses our logic. There are some specific cases, though, where we could cook-up a data structure
where, in some place, instead of Optional we use a default value, and that would remove the need for Affine (for example, instead of Dictionary<Key,Value> we could imagine a DefaultedDictionary<Key,Value>): it’s up to you to choose the right solution for each specific problem.
Conclusion
Lens, Prism and Affine are abstractions over the relationships between a data structure and its parts. They allow to encapsulate such relationships with any level of composition, both vertical (like from a parent to a child of a child) and horizontal (like from a parent to different children in parallel). This relationship can be extended in many different ways: we can induce structure from a child to a parent, like for example in giving ordering logic to a data structure starting from a comparator in one of its parts (it was shown by Brandon Williams in this talk).
The main use case is representing the modifications induced into a data structure by modifying its parts, and composition plays a huge role. A nice, simple use case for prisms is also to assert that an enum is in a particular case, like you would do with guard case but with a single expression, for example with a function like this:
extension Prism {
func isCase(_ whole: Whole) -> Bool {
return tryGet(whole) != nil
}
}
In fact, once you get the basic definition laid out for Lens and Prism, a universe of possibilities opens: we just need to explore it.
Bonus Theory: the Lens/Prism duality
Another piece of trivia that you get when googling about functional lenses and prisms is that “prism is the dual of lens”. The mathematical concept of duality is pretty complex in general, but in this particular case it means that from a lens we can get something else (with different properties) by simply “reversing the arrows”, or in other words, by reversing all the (directed) relationships. For example if we have a function of type:
(A) -> B
The dual of this function is going to be:
(B) -> A
This is not the inverse function of (A) -> B: the inverse function is the function that, applied after the first, gives us back exactly the value with which we started. This is simply a function with switched input and output, and the “dual” procedure simply allows us to discover that such a thing exists (pretty obvious, in this case).
A little more interesting is the dual of a product type: we defined struct and class as product types, in the sense that they’re constructed with a set of properties. The quintessential product type is a tuple, which only has properties (optionally tagged with names in Swift) and no other methods or behavior. A more rigorous way to see this is in term of projections: for every property, we have a function (the getter) from the type of the struct or class to the type of the property. So for example the following type:
struct Product<A,B> {
let a: A
let b: B
}
can be defined completely by the functions:
let projectA: (Product<A,B>) -> A = { $0.a }
let projectB: (Product<A,B>) -> B = { $0.b }
To define a type that’s dual to Product<A,B> we need to turn the projections into injections, like the following:
let injectA: (A) -> ???<A,B> = { ??? }
let injectB: (B) -> ???<A,B> = { ??? }
As many have probably already imagined, the ??? type that actually works in this case is an enum:
enum Coproduct<A,B> {
case a(A)
case b(B)
}
with the injections becoming:
let injectA: (A) -> Coproduct<A,B> = { .a($0) }
let injectB: (B) -> Coproduct<A,B> = { .b($0) }
An enum is thus a coproduct type (co stands for dual to).
Now, we defined lenses for product types, let’s then discover prisms for coproducts as colenses with the same procedure.
First, we need a different representation for Lens<Whole,Part> that’s a little more basic, less convenient but more explicit:
struct Lens<Whole,Part> {
let get: (Whole) -> Part
let set: (Product<Whole,Part>) -> Whole
}
Notice that the set function is not partially applied, and Product<Whole,Part> is just a more explicit way of representing the simple tuple (Whole,Part).
Let’s reverse everything: functions will reverse the arrows, and products become coproducts:
struct ???<Whole,Part> {
let ???: (Part) -> Whole
let ???: (Whole) -> Coproduct<Whole,Part>
}
We’re going to call this Prism. The first function is an injection (it’s the dual of the get projection) so let’s call it inject.
struct Prism<Whole,Part> {
let inject: (Part) -> Whole
let ???: (Whole) -> Coproduct<Whole,Part>
}
The second function is a little more complex: it takes a Whole and returns an enum with two cases:
- the first case is the
Whole again, which means that we really didn’t get anything out of it;
- the second case is
Part, which means that we were able to get what we were looking for.
Thus, let’s call this function tryGet. To achieve the prism representation we used in the article, we can observe that in Coproduct<Whole,Part> the Part case is the only one that’s really interesting, so for what matters to us it could as well be Coproduct<(),Part>; but the latter is basically Optional<Part> (in fact, the none case in Optional implicitly has () as associated type). Finally, by switching the order of the properties we get:
struct Prism<Whole,Part> {
let tryGet: (Whole) -> Part?
let inject: (Part) -> Whole
}
which is the representation we’re been using the whole time. Notice that we could have discovered this simply by starting with Lens and being instructed about how to reverse the arrows.
Until next time.